CNC Machining Conical Ellipses with Double-Nested Macros

The 20th CPC Central Committee calls for top scientists, engineers, and skilled professionals to build a first-class workforce.

High-skilled talent includes those with advanced skills, creativity, and senior or technician-level qualifications.

Growing demand for high-skilled talent raises CNC operator skill requirements, causing a significant shortage of technicians and senior technicians.

Certifying CNC technicians requires processing non-circular curves.

Parts featuring non-circular curves present greater machining challenges compared to those with external circles or arcs.

CNC machines lack non-circular interpolation, so programmers use linear approximation and macro programs to machine complex surfaces.

Conventional CNC programming struggles with conical ellipses.

This paper uses a double-nested macro program to solve the problem and guide future non-circular curve machining.

Basic Knowledge of Ellipses

An ellipse is the path traced by a moving point whose sum of distances from two fixed points remains constant.These fixed points are called the foci of the ellipse.

Standard Equation of an Ellipse

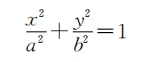
Parametric Equations of an Ellipse

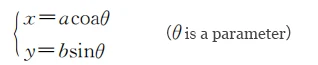
In the parametric equations of an ellipse, the constants a and b represent the major and minor semi-axes, respectively, with a > b.

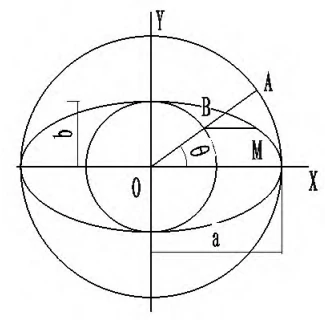
The geometric meaning of parameter θ is the rotation angle of the corresponding major or minor circle radius, i.e., the eccentric angle of the ellipse.

Its range is θ ∈ [0, 2π], determining the coordinates of each point on the ellipse (as shown in Figure 1).

When a specific angle θ is fixed, the parametric equations provide the coordinates of the corresponding points on the ellipse.

For example, the x-coordinate of point M in the figure is x = a cos θ, and the y-coordinate is y = b sin θ.

This equation describes the trajectory of any point on the ellipse.

FANUC Macro Program Knowledge

Macro programs enable the use of variables, arithmetic and logical operations, and conditional jumps, simplifying the creation of machining programs.

Variables

Programmers designate variables using the variable symbol # followed by the variable number.

Variables can be categorized into four types based on their number:

• Variable Types

#0 is a null variable;
#1–#33 are local variables;
#100–#199, #500–#99 are public variables;
#1000 and above are system variables.

• Omitting the Decimal Point

When defining variable values in a program, the decimal point may be omitted.

• Variable References

A variable’s value can be referenced by specifying its number after an address. To change the sign of a referenced variable, place a negative sign before the #.

Operators and Expressions

All constants and variables in macro programs can be represented using operators and expressions.

Common arithmetic operators: +, -, *, /; Conditional operators:

EQ, NE, GT, GE, LT, LE; Logical operators: AND, OR, NOT;

Function operators: SIN, COS, TAN, ASIN, ACOS, ATAN, ABS, SQR, ROUND.

Expressions are formed by combining constants and variables using operators.

Macro Program Statements and NC Statements

The following program segments constitute macro program statements:

Program segments containing macro call instructions;
Program segments containing control statements;
Program segments containing arithmetic or logical operations;
NC statements refer to any other program segments outside of macro programs.

Transfer and Loop Instructions

Within macro programs, when using IF statements and GOTO statements, there are three types of transfer and loop operations:

GOTO statements (unconditional transfer), IF statements (conditional transfer), and WHILE statements (looping when a condition is met).

• Unconditional Transfer (GOTO Statement): If a sequence number outside the range 1 to 99999 is specified, the system will trigger a P/S alarm.
• Conditional Transfer (IF): IF [<condition expression>] GOTO n. A condition expression must follow the IF statement.
• Loop statement (WHILE). A conditional expression follows WHILE.

When the specified condition is met, the program segment between DO and END executes.

If the condition is not met, the segment after END executes.

Note on infinite loops:

If only a DO statement is specified without a WHILE statement, an infinite loop occurs from DO to END.

Zero and <empty>: In conditional expressions not using EQ or NE, <empty> is treated as zero.

Programming Example

The conical ellipse shown in Figure 2 has an elliptical plane and a conical solid.

This document employs a double-nested macro program to program and machine the conical ellipse on a CNC milling machine.

Task Requirements

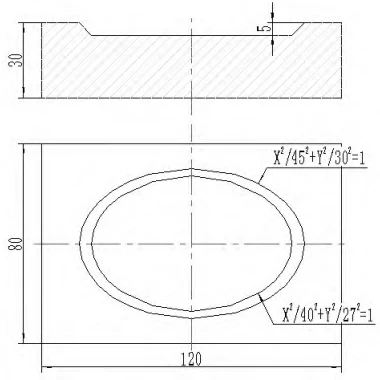
As shown in Figure 3, the workpiece drawing depicts an aluminum component with dimensions 120 mm × 80 mm × 30 mm.

According to the drawing specifications, the program must machine a 5 mm deep conical ellipse onto the surface.

Drawing Analysis

•  Analyzing Geometric Features: The cavity is a conical ellipse, with each Z-axis cross-section forming an ellipse of varying axes.

The upper end has a major axis of 45 mm and a minor axis of 30 mm; the lower end has a major axis of 40 mm and a minor axis of 27 mm.

• Establishing the Mathematical Model: As shown in the figure, the major and minor axes of the ellipse exhibit linear variation.

Specifically, for every 1 mm decrease in the Z-direction, the major and minor axes decrease by (45-40)/5 = 1 mm and (30-27)/5 = 0.6 mm, respectively.

• Determining Variables and Program Output: This programming employs nested double-level macros.

The first level sets Z as the independent variable, with each iteration completing one ellipse. The initial value is Z=0, and the loop exits when Z reaches -5.0.

The second layer processes ellipses with angle θ as the independent variable, initialized at θ = 0. The loop exits when θ = 360.

Process Analysis

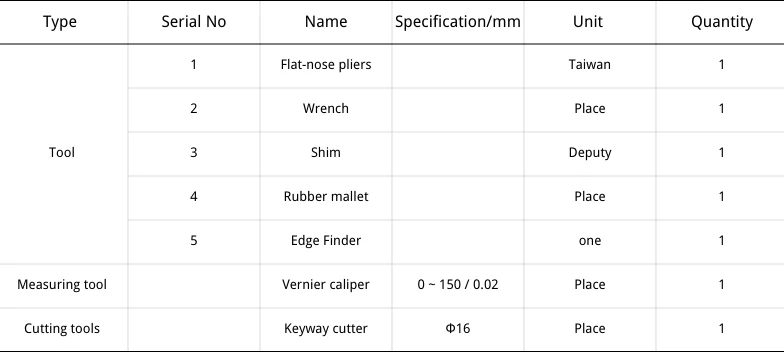
Tools, Gauges, and Cutting Tools

The diagram lacks specs. Machine aluminum with a Φ10 mm keyway cutter from the center and measure with a 0.02 mm vernier caliper.

The technician clamps the square workpiece in a vise and aligns it with a dial indicator (as shown in Table 1).

Process Card Development

Flat milling process card (as shown in Table 2).

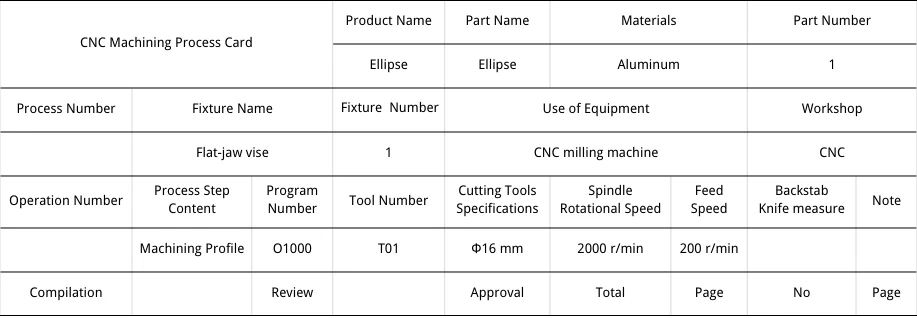
Machining Program

Precautions

• Macro program writing involves numerous symbols and letters. After completion, carefully verify the program for accuracy.

It is best to simulate run it on the CNC milling machine to check correctness before commencing actual machining.

• Install fixtures, workpieces, and cutting tools according to process specifications.
• Initially, reduce feed rate and monitor tool positions to ensure accuracy and avoid collisions.
• During conical ellipse machining, if surface roughness fails to meet requirements, apply these solutions:

Minimize the ellipse’s index angle (Variable #4);
Reduce the Z-axis cutting depth (Variable #1).

Conclusion

Engineers use mathematical methods with linear fitting techniques to machine non-circular curves.

During machining, the program defines the start and end values of the non-circular curve.

Compute the formula and automate curve machining with a macro program.

Machining conical ellipses on CNC mills employs nested macro programs.

The first layer sets the Z-value as the independent variable to achieve layered machining.

While the second layer uses angle θ as the independent variable to complete ellipse machining.

This approach resolves conical ellipse machining challenges on CNC mills.

This paper employs a double-nested macro program for conical ellipse CNC machining.

Based on specific case studies, it explores the application of conical ellipse machining in CNC milling.

This method solves programming challenges and guides future non-circular curve milling.